フレネル
7歳のときに出会って別れ,15歳で再会して別れ,29歳になってまた巡り会った同い年の2人の女性,結珠(ゆず)と果遠(かのん)の友情/愛情,著者曰く 「名前のつけられない関係」が描かれた物語です.
「灯台が好きなの?」
「そういうわけじゃなくて、たまたまスクールの図書室で『灯台の光はなぜ遠くまで届くのか』っていう本を読んだら、面白かったので」
「ふうん。どんなこと書いてあるの?」
「えっと・・・・・・フレネルっていうフランス人が発明したレンズで、灯台はぐっと明るくなって世界中の航海が安全になったっていう歴史です」
「ああ、そっか、単に大きい電球灯せばいいって話じゃないもんね」 (P.332)
フレネルはフランスの土木技師・物理学(光学)者で,今やほとんどの灯台で使われているフレネルレンズを発明した人として有名です.実際に発行されている『灯台の光はなぜ遠くまで届くのか』という本も読んでみました.フレネルレンズ発明のおかげで,その後多くの人の命が守られたそうです.
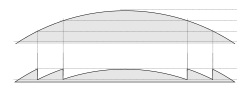 |
| 上が凸レンズ,下がフレネルレンズ (Wikipedia) |
数学では光の強度等の計算に応用されているフレネル積分が有名です.この積分は次の式で表されます.$$S(x)=\int_0^x \sin{t^2} dt\quad\quad\quad C(x)=\int_0^x \cos{t^2} dt\tag{1}$$式 (1) は原始関数(=不定積分)ですが,次の定積分の極限(広義積分)もフレネル積分といいます.$$\int_{-\infty}^\infty \sin{x^2} dx=\int_{-\infty}^\infty \cos{x^2} dx=\sqrt{\frac{\pi}{2}}\tag{2}$$あるいは式 (2) をオイラーの公式 $\cos x+i\sin x=e^{ix}$ の形でまとめて,次のように表すこともあります.$$\int_{-\infty}^\infty e^{i x^2} dx=\sqrt{\frac{\pi}{2}}(1+i)=\sqrt{i\pi}$$
小説「イコ トラベリング 1948-」のところで正規化・非正規化の話をしました.上の式 (2) は非正規ですが,スケールを変えて次式にすれば全区間の積分が1になって正規化されます.$$\int_{-\infty}^\infty \sin{\frac{\pi x^2}{2}} dx=\int_{-\infty}^\infty \cos{\frac{\pi x^2}{2}} dx=1$$
フレネル積分は一見簡単そうな式に見えますが,不定積分は式 (1) でしか表せないし,式 (2) の値は複素積分を使って導出するので意外に複雑です.
次の積分は高校数学Ⅲを既習なら導出できますが,フレネル積分と混同しないように気をつけましょう.\begin{eqnarray}\int_0^{\frac{\pi}{2}} \sin^2{x}\ dx &=& \int_0^{\frac{\pi}{2}} \frac{1-\cos{2x}}{2} \ dx\\ &=&\left[ \frac{x}{2}-\frac{1}{4}\sin{2x}\right]_0^{\frac{\pi}{2}}\\&=&\frac{\pi}{4}\end{eqnarray}因みにこの積分は,次のウォリス積分の式の n=2 のときのものになります.なぜ,これだけ積分区間が0から$\frac{\pi}{2}$になっているかというと,$\frac{\pi}{2}$ずつ絶対値の等しい値が繰り返されるからです.$$\int_0^{\frac{\pi}{2}} \sin^n{x}\ dx=\int_0^{\frac{\pi}{2}} \cos^n{x}\ dx$$
ところで,第3章の舞台だった和歌山県の串本町は何度も行ったことがあり,実際に知っている場所がいくつも出てきたので,それらの景色や施設が思い出され,読む前に予期しなかったことで楽しむことができました.
[参考]
灯台の光はなぜ遠くまで届くのか
テレサ・レヴィット (著) 岡田好惠 (翻訳) 2015年 講談社
フレネル積分(sin(x^2)の積分)とその導出証明
https://mathlandscape.com/fresnel-integral/
ナイフエッジからの回折
https://www.fbs.osaka-u.ac.jp/labs/ishijima/Diffraction-32.html

0 件のコメント:
コメントを投稿