小説 風が強く吹いている

三浦 しおん　2006年　新潮社

楕円
----
ひさしく覚えなかった高揚が、走（かける）の心と体を震わせた。
だがここは、永遠の楕円を描く競技場のトラックではない。
----
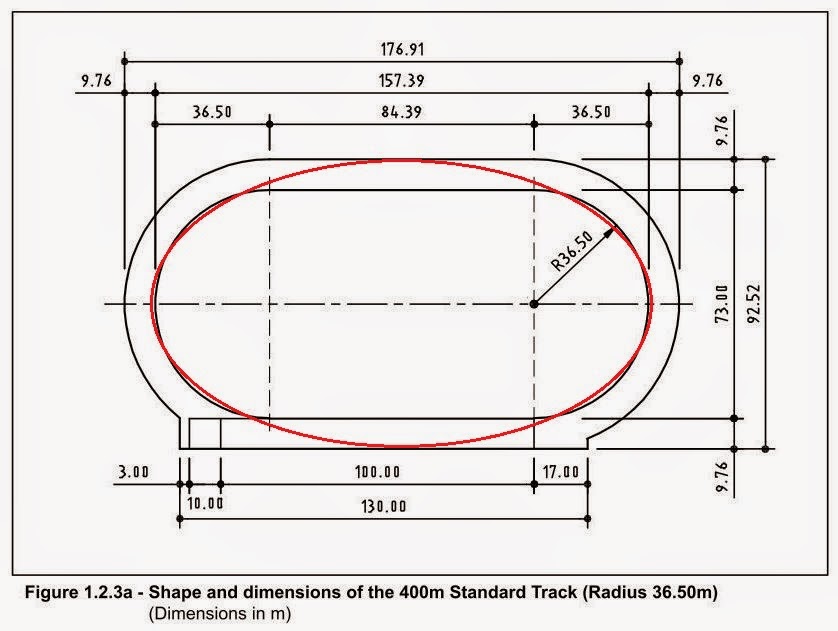
　陸上競技のトラックは楕円(ellipse)というより楕円状(oval)ですね。国際陸上競技連盟(International Association of Athletics Federations = IAAF)の公認トラックは線分2本と半円2個でできていて、線分の長さが84.39m、円の半径が36.50m。円の外側0.30mのところを走って1周400mになるようにしているので、その計算は次のようになります。
84.39×2＋2π×36.80＝400.00m
　もしトラックが本物の楕円ならどうなるでしょうか。長軸をa、短軸をbとすると楕円の媒介変数表示は
x=acost, y=bsint
となります。公認トラックの端から端＋0.3m×2の距離が
2a=84.39＋36.80×2＝157.99m

なので、この1/2のa=78.995mの長軸を持つ楕円で周長が400mになるものを求めてみましょう。楕円の面積はπabと簡単に求められるのですが、周長は難しい計算になります。媒介変数表示の曲線の長さの公式より
4∫[0 to π/2](Sqrt(a^2(cost)^2+b^2(sint)^2)dt＝400
を解けばいいのですが、これは第二種完全楕円積分といって初等的な計算では求められません。そこでグラフ電卓を使って求めると、短軸が46.17mになりました。この楕円を実際のトラックに重ねてみると図のようになります。公認トラックの図はIAAF official websiteから引用しましたが、そこではoval trackとなっていました。図の下のキャプションは、「図1.2.3A 400m標準トラック（半径36.50m）の形と寸法（単位はm）」という意味です。

アニメ デュラララ!!×2承 第6話

成田良悟(原作)　2010年　MBS

解析概論　十二進法　忌み数字
　ロシア人女性の殺し屋ヴァローナが、まるで雑誌をめくるようにあの難しい解析概論を読みながら、13がなぜ不吉な数と言われるのかを説明していました。
--------

諸説存在します。最後の晩餐、ユダの座った13番目の席が有名。ただし、キリスト教だけが原典にあらず。

北欧の神々の伝承、12人の神による調和、13番目に現れたロキが調和を乱した。
古代、12進法を使っていた国々、13番目は12の調和を破壊、忌み数字。
--------
　1, 2, 3, 4, 6, 12と約数の多い12は調和を意味する数とされていたため、その12に1を加えた素数13は調和を乱すと考えられていたようです。この13は忌み数または忌み数字、英語ではbaker's dozen, devil's dozen, witch's dozenとも呼ばれています。

　ヴァローナが読んでいた解析概論は、日本の数学界ではバイブルともいえる本で、日本初の世界的数学者である髙木貞二が書いたものです。大学の理系の教科書としてよく使われていて、第1版は1938年発行、私は1975年の第17刷を持っています。このアニメのようにとてもペラペラとめくりながら読める本ではありません。表紙が緑色がかっていたので、改訂第3版軽装版だと思われます。内容がはっきりわかるほど細かく描写されていたので、思わずそのページを調べてしまいました。P.16-17をめくって24-25、28-29をめくって30-31、144-145をめくって304-305をめくって328-329でした。つまり、めくっているのにページ数は飛んでいました。こんな細かいところまで調べるような人は他にいないだろうと思ったら、こちらにいました（笑）。

ドラマ スペシャリスト3

ハノイの塔

上からアルファベットの文字が"cosidemple"と書かれてある10段のハノイの塔の操作中、51手目の状態が"simple code"になり、これが事件解決ためのヒントになるという話です。

n段のハノイの塔の最小移動回数f(n)は2^n-1になりますが、まずこれを求める漸化式の解き方が画面に出ます。n段の移動には、①まずn-1段を移動する（f(n-1)手）、②一番下のn段目を移動する（1手）、③またn-1段を移動する（f(n-1)手）という操作になるので、漸化式はそれらの和で次のようになります。
f(n)=2f(n-1)+1
これを解くと、
f(n)=2^1(2f(n-2)+1)+1
=2^2(2f(n-3)+1)+2+1
=2^3f(n-3)+2^2+2+1
…
=2^(n-1)f(1)+2^(n-2)+2^(n-3)+…+2+1
=2^(n-1)+2^(n-1)-1
=2^n-1
よって、f(n)=2^n-1となりますが、ドラマでは主人公がこの式を知っていたようで、2^n-1から紙に書き始めます。
2^n-1
2^10-1=2×2×2×…×2×2-1
=1024-1
=1023
その後、なぜかいきなり
2^5+2^4+2^1+2^0
51
と計算して、「51手」とつぶやき、10段のハノイの塔を実際に操作して、51手目の状態が"simple code"になることに気がつきます。
ただ、これは実際に操作しなくても計算で次のように求めることができます。
f(1)=1, f(2)=3, f(3)=7, f(4)=15, f(5)=31, f(6)=63
ですから、51=f(6)の途中=f(5)+20=f(5)+1+19=f(5)+1+f(5)の途中=f(5)+1+f(4)+4=f(5)+1+f(4)+1+3=f(5)+1+f(4)+1+f(2)
すなわち、まず31手で上の5段を移し、次の1手（32手目）で6段目を移し、次の15手（47手目まで）で上の4段を移し、次の1手（48手目）で5段目を移し、あと3手（51手目まで）で上の2段を移します。これでどんな状態になるかを分かり易く右図にまとめてみました。（WolframAlphaで"Tower of Hanoi 10-disk 51 step"と入力したらちゃんと51手目の状態が表示されました。WolframAlphaはすごい！）

それにしても，主人公がなぜ2^5+2^4+2^1+2^0を理解したのかが疑問に残りました。